(related to Problem: The Dissected Triangle)
Diagram $A$ is our original triangle. We will say it measures $5$ inches (or $5$ feet) on each side. If we take off a slice at the bottom of an equilateral triangle by a cut parallel with the base, the portion that remains will always be an equilateral triangle; so we first cut off piece $1$ and get a triangle $3$ inches on every side. The manner of finding directions of the other cuts in $A$ is obvious from the diagram.
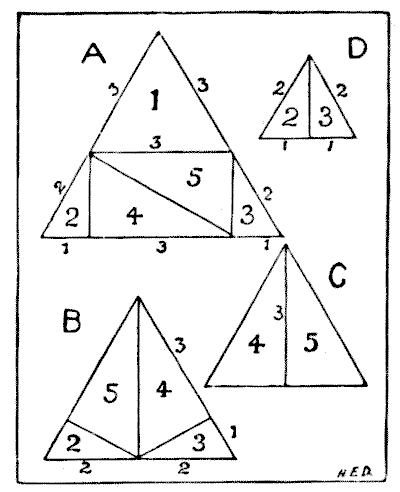
Now, if we want two triangles, $1$ will be one of them, and $2,$ $3,$ $4,$ and $5$ will fit together, as in $B,$ to form the other. If we want three equilateral triangles, $1$ will be one, $4$ and $5$ will form the second, as in $C,$ and $2$ and $3$ will form the third, as in $D.$ In $B$ and $C$ the piece $5$ is turned over; but there can be no objection to this, as it is not forbidden, and is in no way opposed to the nature of the puzzle.
This eBook is for the use of anyone anywhere in the United States and most other parts of the world at no cost and with almost no restrictions whatsoever. You may copy it, give it away or re-use it under the terms of the Project Gutenberg License included with this edition or online at http://www.gutenberg.org. If you are not located in the United States, you'll have to check the laws of the country where you are located before using this ebook.