(related to Problem: The Joiner's Problem)
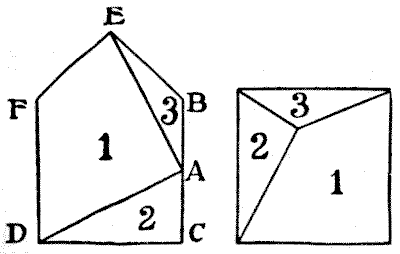
Nothing could be easier than the solution to this puzzle — when you know how to do it. And yet it is apt to perplex the novice a good deal if he wants to do it in the fewest possible pieces — three. All you have to do is to find the point $A,$ midway between $B$ and $C,$ and then cut from $A$ to $D$ and from $A$ to $E.$ The three pieces then form a square in the manner shown. Of course, the proportions of the original figure must be correct; thus the triangle $BEF$ is just a quarter of the square $BCDF.$ Draw lines from $B$ to $D$ and from $C$ to $F$ and this will be clear.
This eBook is for the use of anyone anywhere in the United States and most other parts of the world at no cost and with almost no restrictions whatsoever. You may copy it, give it away or re-use it under the terms of the Project Gutenberg License included with this edition or online at http://www.gutenberg.org. If you are not located in the United States, you'll have to check the laws of the country where you are located before using this ebook.