(related to Problem: The Potato Puzzle)
As many as twenty-two pieces may be obtained by the six cuts. The illustration shows a pretty symmetrical solution. The rule in such cases is that every cut shall intersect every other cut and no two intersections coincide; that is to say, every line passes through every other line, but more than two lines do not cross at the same point anywhere. There are other ways of making the cuts, but this rule must always be observed if we are to get the full number of pieces.
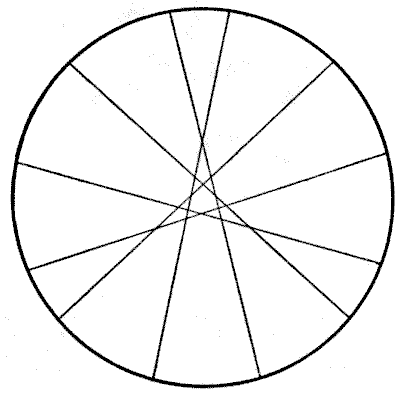
The general formula is that with $n$ cuts we can always produce $$\frac{(n(n + 1) + 1)}{2}.$$ One of the problems proposed by the late Sam Loyd was to produce the maximum number of pieces by $n$ straight cuts through a solid cheese. Of course, again, the pieces cut off may not be moved or piled. Here we have to deal with the intersection of planes (instead of lines), and the general formula is that with $n$ cuts we may produce $$\frac{((n - 1)n(n + 1))}{6} + n + 1$$ pieces. It is extremely difficult to "see" the direction and effects of the successive cuts for more than a few of the lowest values of $n.$
This eBook is for the use of anyone anywhere in the United States and most other parts of the world at no cost and with almost no restrictions whatsoever. You may copy it, give it away or re-use it under the terms of the Project Gutenberg License included with this edition or online at http://www.gutenberg.org. If you are not located in the United States, you'll have to check the laws of the country where you are located before using this ebook.