(related to Problem: The Square of Veneer)
Any square number may be expressed as the sum of two squares in an infinite number of different ways. The solution of the present puzzle forms a simple demonstration of this rule. It is a condition that we give actual dimensions.
In this puzzle, I ignore the known dimensions of our square and work on the assumption that it is $13n$ by $13n.$ The value of n we can afterwards determine. Divide the square as shown (where the dotted lines indicate the original markings) into $169$ squares. As $169$ is the sum of the two squares $144$ and $25,$ we will proceed to divide the veneer into two squares, measuring respectively $12\times12$ and $5\times5;$ and as we know that two squares may be formed from one square by dissection in four pieces, we seek a solution in this number. The dark lines in the diagram show where the cuts are to be made. The square $5\times5$ is cut out whole, and the larger square is formed from the remaining three pieces, $B, C,$ and $D,$ which the reader can easily fit together.
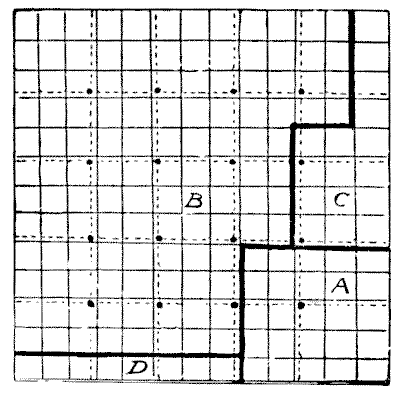
Now, $n$ is clearly $\frac{5}{13}$ of an inch. Consequently, our larger square must be $\frac{60}{13} \times \frac{60}{13}$ in., and our smaller square $\frac{25}{13} \times \frac{25}{13}$ in. The square of $\frac{60}{13}$ added to the square of $\frac{25}{13}$ is 25. The square is thus divided into as few as four pieces that form two squares of known dimensions, and all the sixteen nails are avoided.
Here is a general formula for finding two squares whose sum shall equal a given square, say $a^2.$ In the case of the solution of our puzzle $p = 3,$ $q = 2,$ and $a = 5$:
$$\frac{2pqa}{p^2+q^2}=x,\quad\quad\frac{\sqrt{a^2( p^2 + q^2)^2 - (2pqa)^2}}{p^2 + q^2} =y.$$
Here $x^2 + y^2 = a^2.$
This eBook is for the use of anyone anywhere in the United States and most other parts of the world at no cost and with almost no restrictions whatsoever. You may copy it, give it away or re-use it under the terms of the Project Gutenberg License included with this edition or online at http://www.gutenberg.org. If you are not located in the United States, you'll have to check the laws of the country where you are located before using this ebook.