(related to Problem: Concerning Wheels)
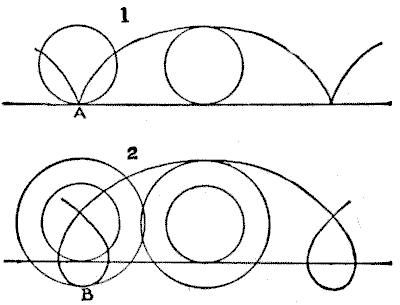
If you mark a point $A$ on the circumference of a wheel that runs on the surface of a level road, like an ordinary cart-wheel, the curve described by that point will be a common cycloid, as in Fig. $1.$ But if you mark a point $B$ on the circumference of the flange of a locomotive-wheel, the curve will be a curtate cycloid, as in Fig. $2,$ terminating in nodes. Now, if we consider one of these nodes or loops, we shall see that "at any given moment" certain points at the bottom of the loop must be moving in the opposite direction to the train. As there is an infinite number of such points on the flange's circumference, there must be an infinite number of these loops being described while the train is in motion. In fact, at any given moment certain points on the flanges are always moving in a direction opposite to that in which the train is going.
In the case of the two wheels, the wheel that runs around the stationary one makes two revolutions around its own center. As both wheels are of the same size, it is obvious that if at the start we mark a point on the circumference of the upper wheel, at the very top, this point will be in contact with the lower wheel at its lowest part when half the journey has been made. Therefore this point is again at the top of the moving wheel, and one revolution has been made. Consequently, there are two such revolutions in the complete journey.
This eBook is for the use of anyone anywhere in the United States and most other parts of the world at no cost and with almost no restrictions whatsoever. You may copy it, give it away or re-use it under the terms of the Project Gutenberg License included with this edition or online at http://www.gutenberg.org. If you are not located in the United States, you'll have to check the laws of the country where you are located before using this ebook.