(related to Problem: Lady Belinda's Garden)
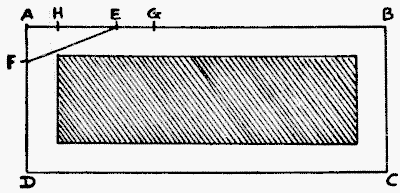
All that Lady Belinda need do was this: She should measure from $A$ to $B,$ fold her tape in four and mark off the point E, which is thus one-quarter of the side. Then, in the same way, mark off the point $F,$ one-fourth of the side $AD$ Now, if she makes $EG$ equal to $AF,$ and $GH$ equal to $EF,$ then $AH$ is the required width for the path in order that the bed shall be exactly half the area of the garden. An exact numerical measurement can only be obtained when the sum of the squares of the two sides is a square number. Thus, if the garden measured $12$ poles by $5$ poles (where the squares of $12$ and $5,$ $144$ and $25,$ sum to $169,$ the square of $13$), then $12$ added to $5,$ less $13,$ would equal four, and a quarter of this, $1$ pole, would be the width of the path.
This eBook is for the use of anyone anywhere in the United States and most other parts of the world at no cost and with almost no restrictions whatsoever. You may copy it, give it away or re-use it under the terms of the Project Gutenberg License included with this edition or online at http://www.gutenberg.org. If you are not located in the United States, you'll have to check the laws of the country where you are located before using this ebook.