(related to Problem: The Compasses Puzzle)
Let $AB$ in the following diagram be the given straight line With the centers $A$ and $B$ and radius $AB$ describe the two circles. Mark off $DE$ and $EF$ equal to $AD.$ With the centers $A$ and $F$ and radius $DF$ describe arcs intersecting at $G.$ With the centers $A$ and $B$ and distance $BG$ describe arcs $GHK$ and $N.$ Make $HK$ equal to $AB$ and $HL$ equal to $HB.$ Then with centres $K$ and $L$ and radius $AB$ describe arcs intersecting at $I.$ Make $BM$ equal to $BI$. Finally, with the center $M$ and radius $MB$ cut the line in $C,$ and the point $C$ is the required middle of the line $AB.$ For greater exactitude you can mark off $R$ from $A$ (as you did $M$ from $B$), and from $R$ describe another arc at $C.$ This also solves the problem, to find a point midway between two given points without the straight line.
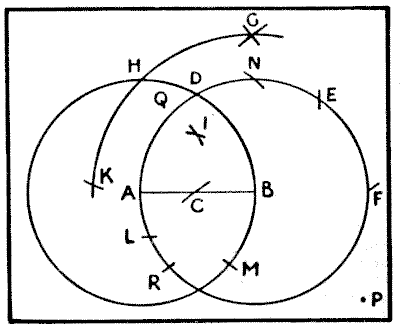
I will put the young geometer in the way of a rigid proof. First prove that twice the square of the line $AB$ equals the square of the distance BG, from which it follows that $HABN$ are the four corners of a square. To prove that $I$ is the center of this square, draw a line from $H$ to $P$ through $QIB$ and continue the arc $HK$ to $P.$ Then, conceiving the necessary lines to be drawn, the angle $HKP,$ being in a semicircle, is a right angle. Let fall the perpendicular $KQ,$ and by similar triangles, and from the fact that $HKI$ is an isosceles triangle by the construction, it can be proved that $HI$ is half of $HB.$ We can similarly prove that $C$ is the center of the square of which $AIB$ are three corners.
I am aware that this is not the simplest possible solution.
This eBook is for the use of anyone anywhere in the United States and most other parts of the world at no cost and with almost no restrictions whatsoever. You may copy it, give it away or re-use it under the terms of the Project Gutenberg License included with this edition or online at http://www.gutenberg.org. If you are not located in the United States, you'll have to check the laws of the country where you are located before using this ebook.