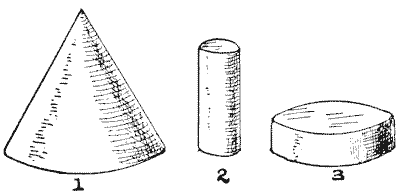
I have a wooden cone, as shown in Fig. 1. How am I to cut out of it the greatest possible cylinder? It will be seen that I can cut out one that is long and slender, like Fig. 2, or short and thick, like Fig. 3. But neither is the largest possible. A child could tell you where to cut, if he knew the rule. Can you find this simple rule?
Solutions: 1
This eBook is for the use of anyone anywhere in the United States and most other parts of the world at no cost and with almost no restrictions whatsoever. You may copy it, give it away or re-use it under the terms of the Project Gutenberg License included with this edition or online at http://www.gutenberg.org. If you are not located in the United States, you'll have to check the laws of the country where you are located before using this ebook.