(related to Problem: The Yorkshire Estates)
The triangular piece of land that was not for sale contains exactly eleven acres. Of course it is not difficult to find the answer if we follow the eccentric and tricky tracks of intricate trigonometry; or I might say that the application of a well-known formula reduces the problem to finding one-quarter of the square root of $$(4 \times 370 \times 116) - (370 + 116 - 74)^2$$ — that is a quarter of the square root of $1936,$ which is one-quarter of $44,$ or $11$ acres. But all that the reader really requires to know is the Pythagorean law on which many puzzles have been built, that in any right-angled triangle the square of the hypotenuse is equal to the sum of the squares of the other two sides. I shall dispense with all "surds" and similar absurdities, notwithstanding the fact that the sides of our triangle are clearly incommensurate, since we cannot exactly extract the square roots of the three square areas.
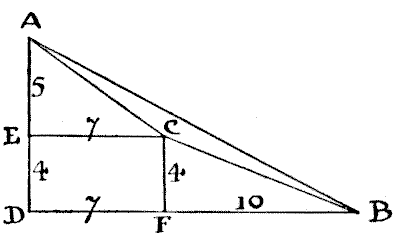
In the above diagram, $ABC$ represents our triangle. $ADB$ is a right-angled triangle, $AD$ measuring $9$ and $BD$ measuring $17,$ because the square of $9$ added to the square of $17$ equals $370,$ the known area of the square on $AB.$ Also $AEC$ is a right-angled triangle, and the square of $5$ added to the square of $7$ equals $74,$ the square estate on $A C.$ Similarly, $CFB$ is a right-angled triangle, for the square of $4$ added to the square of $10$ equals $116,$ the square estate on $BC.$ Now, although the sides of our triangular estate are incommensurate, we have in this diagram all the exact figures that we need to discover the area with precision.
The area of our triangle $ADB$ is clearly half of $9 \times 17,$ or $76\frac 12$ acres. The area of $AEC$ is half of $5 \times 7,$ or $17\frac 12$ acres; the area of $CFB$ is half of $4\times 10,$ or $20$ acres; and the area of the oblong $EDFC$ is obviously $4 \times 7,$ or $28$ acres. Now, if we add together $17\frac 12,$ $20,$ and $28 = 65\frac 12,$ and deduct this sum from the area of the large triangle $ADB$ (which we have found to be $76\frac 12$ acres), what remains must clearly be the area of $ABC.$ That is to say, the area we want must be $76\frac 12 - 65\frac 12 = 11$ acres exactly.
This eBook is for the use of anyone anywhere in the United States and most other parts of the world at no cost and with almost no restrictions whatsoever. You may copy it, give it away or re-use it under the terms of the Project Gutenberg License included with this edition or online at http://www.gutenberg.org. If you are not located in the United States, you'll have to check the laws of the country where you are located before using this ebook.