(related to Problem: Two New Magic Squares)
Here are two solutions that fulfill the conditions:—
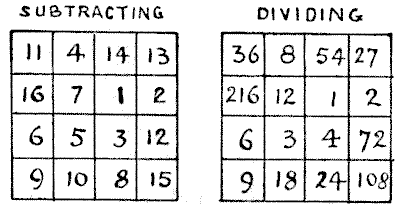
The first, by subtracting, has a constant $8,$ and the associated pairs all have a difference of $4.$ The second square, by dividing, has a constant $9,$ and all the associated pairs produce $3$ by division. These are two remarkable and instructive squares.
This eBook is for the use of anyone anywhere in the United States and most other parts of the world at no cost and with almost no restrictions whatsoever. You may copy it, give it away or re-use it under the terms of the Project Gutenberg License included with this edition or online at http://www.gutenberg.org. If you are not located in the United States, you'll have to check the laws of the country where you are located before using this ebook.