(related to Problem: The Baskets Of Plums)
As the merchant told his man to distribute the contents of one of the baskets of plums "among some children," it would not be permissible to give the complete basketful to one child; and as it was also directed that the man was to give "plums to every child, so that each should receive an equal number," it would also not be allowed to select just as many children as there were plums in a basket and give each child a single plum. Consequently, if the number of plums in every basket was a prime number, then the man would be correct in saying that the proposed distribution was quite impossible. Our puzzle, therefore, resolves itself into forming a magic square with nine different prime numbers.
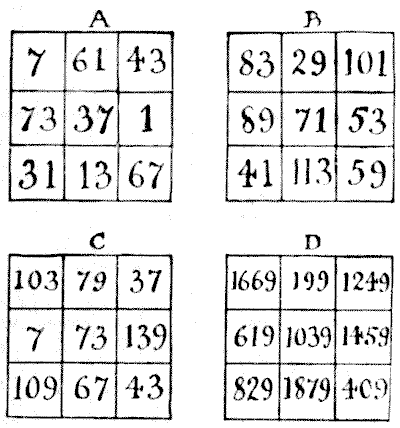
In Diagram $A$ we have a magic square in prime numbers, and it is the one giving the smallest constant sum that is possible. As to the little trap I mentioned, it is clear that Diagram $A$ is barred out by the words "every basket contained plums," for one plum is not plums. And as we were referred to the baskets, "as shown in the illustration," it is perfectly evident, without actually attempting to count the plums, that there are at any rate more than $7$ plums in every basket. Therefore $C$ is also, strictly speaking, barred. Numbers over $20$ and under, say, $250$ would certainly come well within the range of possibility, and a large number of arrangements would come within these limits. Diagram $B$ is one of them. Of course, we can allow for the false bottoms that are so frequently used in the baskets of fruitsellers to make the basket appear to contain more fruit than it really does.
Several correspondents assumed (on what grounds I cannot think) that in the case of this problem the numbers cannot be in consecutive arithmetical progression, so I give Diagram $D$ to show that they were mistaken. The numbers are $199,$ $409,$ $619,$ $829,$ $1,039,$ $1,249,$ $1,459,$ 1,669, and $1,879$ — all primes with a common difference of $210.$
This eBook is for the use of anyone anywhere in the United States and most other parts of the world at no cost and with almost no restrictions whatsoever. You may copy it, give it away or re-use it under the terms of the Project Gutenberg License included with this edition or online at http://www.gutenberg.org. If you are not located in the United States, you'll have to check the laws of the country where you are located before using this ebook.