(related to Problem: The Magic Knight's Tour)
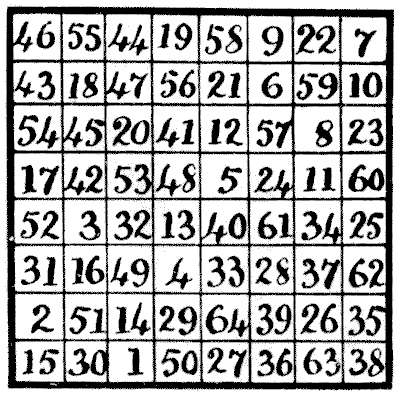
Here each successive number (in numerical order) is a knight's move from the preceding number, and as $64$ is a knight's move from $1,$ the tour is "re-entrant." All the columns and rows add up $260.$ Unfortunately, it is not a perfect magic square, because the diagonals are incorrect, one adding up $264$ and the other $256$ — requiring only the transfer of $4$ from one diagonal to the other. I think this is the best result that has ever been obtained (either re-entrant or not), and nobody can yet say whether a perfect solution is possible or impossible.
This eBook is for the use of anyone anywhere in the United States and most other parts of the world at no cost and with almost no restrictions whatsoever. You may copy it, give it away or re-use it under the terms of the Project Gutenberg License included with this edition or online at http://www.gutenberg.org. If you are not located in the United States, you'll have to check the laws of the country where you are located before using this ebook.