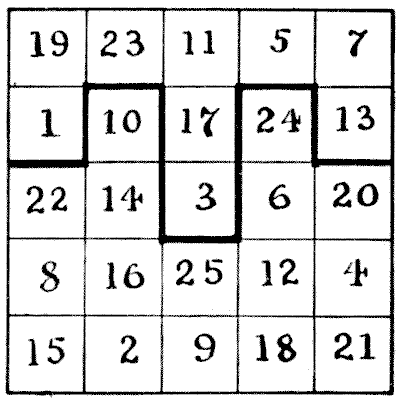
(related to Problem: The Mandarin's "T" Puzzle)
There are many different ways of arranging the numbers, and either the $2$ or the $3$ may be omitted from the "T" enclosure. The arrangement that I give is a "nasik" square. Out of the total of $28,800$ nasik squares of the fifth order this is the only one (with its one reflection) that fulfils the "T" condition. This puzzle was suggested to me by Dr. C. Planck.
This eBook is for the use of anyone anywhere in the United States and most other parts of the world at no cost and with almost no restrictions whatsoever. You may copy it, give it away or re-use it under the terms of the Project Gutenberg License included with this edition or online at http://www.gutenberg.org. If you are not located in the United States, you'll have to check the laws of the country where you are located before using this ebook.