Make a diagram, on a large sheet of paper, like the illustration, and have three counters marked $A,$ three marked $B,$ and three marked $C.$
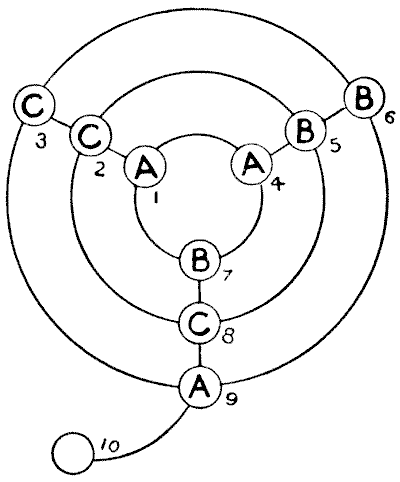
It will be seen that at the intersection of lines there are nine stopping-places, and a tenth stopping-place is attached to the outer circle like the tail of a $Q.$ Place the three counters or engines marked $A,$ the three marked $B,$ and the three marked $C$ at the places indicated.
The puzzle is to move the engines, one at a time, along the lines, from stopping-place to stopping-place, until you succeed in getting an $A,$ a $B,$ and a $C$ on each circle, and also $A,$ $B,$ and $C$ on each straight line. You are required to do this in as few moves as possible. How many moves do you need?
Solutions: 1
This eBook is for the use of anyone anywhere in the United States and most other parts of the world at no cost and with almost no restrictions whatsoever. You may copy it, give it away or re-use it under the terms of the Project Gutenberg License included with this edition or online at http://www.gutenberg.org. If you are not located in the United States, you'll have to check the laws of the country where you are located before using this ebook.