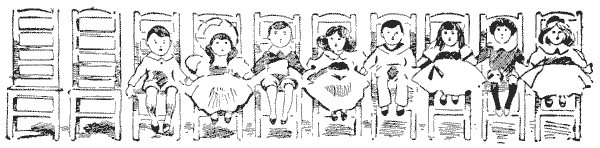
If you mark off ten divisions on a sheet of paper to represent the chairs and use eight numbered counters for the children, you will have a fascinating pastime. Let the odd numbers represent boys and even numbers girls, or you can use counters of two colors or coins.
The puzzle is to remove two children who are occupying adjoining chairs and place them in two empty chairs, making them first change sides; then remove a second pair of children from adjoining chairs and place them in the two now vacant, making them change sides; and so on, until all the boys are together and all the girls together, with the two vacant chairs at one end as at present. To solve the puzzle you must do this in five moves. The two children must always be taken from chairs that are next to one another; and remember the important point of making the two children change sides, as this latter is the distinctive feature of the puzzle. By "change sides" I simply mean that if for example, you first move $1$ and $2$ to the vacant chairs, then the first (the outside) chair will be occupied by $2$ and the second one by $1.$
Solutions: 1
This eBook is for the use of anyone anywhere in the United States and most other parts of the world at no cost and with almost no restrictions whatsoever. You may copy it, give it away or re-use it under the terms of the Project Gutenberg License included with this edition or online at http://www.gutenberg.org. If you are not located in the United States, you'll have to check the laws of the country where you are located before using this ebook.