Here is a rather entertaining little puzzle with moving counters. You only need twelve counters — six of one colour, marked $A, C, E, G, I,$ and $K,$ and the other six marked $B, D, F, H, J,$ and $L.$ You first place them on the diagram, as shown in the illustration, and the puzzle is to get them into regular alphabetical order, as follows:— \[\begin{array}{cccc} A&B&C&D\\ E&F&G&H\\ I&J&K&L \end{array}\]
The moves are made by exchanges of opposite colors standing on the same line. Thus, $G$ and $J$ may exchange places, or $F$ and $A,$ but you cannot exchange $G$ and $C,$ or $F$ and $D,$ because in one case they are both white and in the other case both black. Can you bring about the required arrangement in seventeen exchanges?
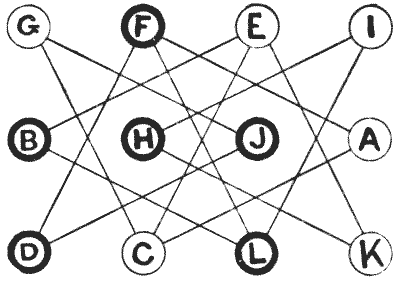
It cannot be done in fewer moves. The puzzle is really much easier than it looks if properly attacked.
Solutions: 1
This eBook is for the use of anyone anywhere in the United States and most other parts of the world at no cost and with almost no restrictions whatsoever. You may copy it, give it away or re-use it under the terms of the Project Gutenberg License included with this edition or online at http://www.gutenberg.org. If you are not located in the United States, you'll have to check the laws of the country where you are located before using this ebook.