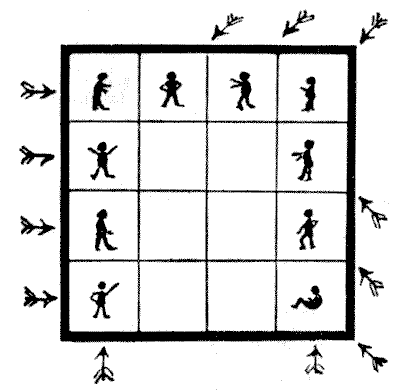
If prisons had no other use, they might still be preserved for the special benefit of puzzle-makers. They appear to be an inexhaustible mine of perplexing ideas. Here is a little poser that will perhaps interest the reader for a short period. We have in the illustration a prison of sixteen cells. The locations of the ten prisoners will be seen. The jailer has queer superstitions about odd and even numbers, and he wants to rearrange the ten prisoners so that there shall be as many even rows of men, vertically, horizontally, and diagonally, as possible. At present, it will be seen, as indicated by the arrows, that there are only twelve such rows of $2$ and $4.$ I will state at once that the greatest number of such rows that is possible is sixteen. But the jailer only allows four men to be removed to other cells and informs me that, as the man who is seated in the bottom right-hand corner is infirm, he must not be moved. Now, how are we to get those sixteen rows of even numbers under such conditions?
Solutions: 1
This eBook is for the use of anyone anywhere in the United States and most other parts of the world at no cost and with almost no restrictions whatsoever. You may copy it, give it away or re-use it under the terms of the Project Gutenberg License included with this edition or online at http://www.gutenberg.org. If you are not located in the United States, you'll have to check the laws of the country where you are located before using this ebook.