Here you pick out the nine cards, ace to nine of diamonds, and arrange them in the form of a triangle, exactly as shown in the illustration so that the pips add up the same on the three sides. In the example given it will be seen that they sum to 20 on each side, but the particular number is of no importance so long as it is the same on all three sides. The puzzle Pg 116is to find out in just how many different ways this can be done.
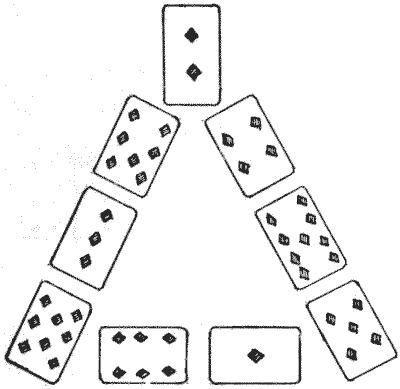
If you simply turn the cards around so that one of the other two sides is nearest to you this will not count as different, for the order will be the same. Also, if you make the $4, 9, 5$ change places with the $7, 3, 8,$ and at the same time exchange the $1$ and the $6,$ it will not be different. But if you only change the $1$ and the $6$ it will be different, because the order around the triangle is not the same. This explanation will prevent any doubt arising as to the conditions.
Solutions: 1
This eBook is for the use of anyone anywhere in the United States and most other parts of the world at no cost and with almost no restrictions whatsoever. You may copy it, give it away or re-use it under the terms of the Project Gutenberg License included with this edition or online at http://www.gutenberg.org. If you are not located in the United States, you'll have to check the laws of the country where you are located before using this ebook.