(related to Problem: The Card Frame Puzzle)
The sum of all the pips on the ten cards is $55.$ Suppose we are trying to get $14$ pips on every side. Then $4$ times $14$ is $56.$ But each of the four corner cards is added in twice so that $55$ deducted from $56,$ or $1,$ must represent the sum of the four corner cards. This is clearly impossible; therefore $14$ is also impossible. But suppose we came to trying $18.$ Then $4$ times $18$ is $72,$ and if we deduct $55$ we get $17$ as the sum of the corners. We need then only try different arrangements with the four corners always summing to $17,$ and we soon discover the following solution:—
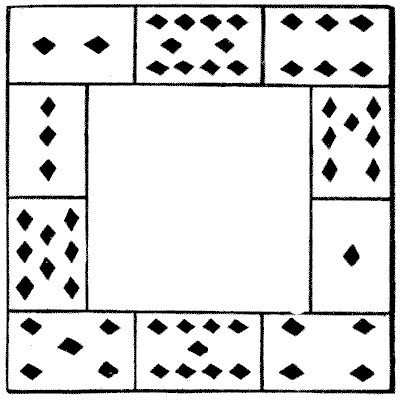
The final trials are very limited in number, and must with a little judgment either bring us to a correct solution or satisfy us that a solution is impossible under the conditions we are attempting. The two center cards on the upright sides can, of course, always be interchanged, but I do not call these different solutions. If you reflect in a mirror you get another arrangement, which also is not considered different. In the answer given, however, we may exchange the $5$ with the $8$ and the $4$ with the $1.$ This is a different solution. There are two solutions with $18,$ four with $19,$ two with $20,$ and two with $22$ — ten arrangements in all. Readers may like to find all these for themselves.
This eBook is for the use of anyone anywhere in the United States and most other parts of the world at no cost and with almost no restrictions whatsoever. You may copy it, give it away or re-use it under the terms of the Project Gutenberg License included with this edition or online at http://www.gutenberg.org. If you are not located in the United States, you'll have to check the laws of the country where you are located before using this ebook.