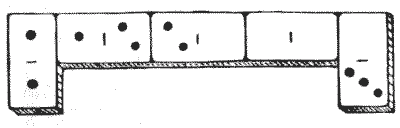
Here is a new little puzzle that is not difficult, but will probably be found entertaining by my readers. It will be seen that the five dominoes are so arranged in proper sequence (that is, with 1 against 1, 2 against 2, and so on), that the total number of pips on the two end dominoes is five, and the sum of the pips on the three dominoes in the middle is also five. There are just three other arrangements giving five for the additions. They are: —
$(1—0)$ $(0—0)$ $(0—2)$ $(2—1)$ $(1—3)$
$(4—0)$ $(0—0)$ $(0—2)$ $(2—1)$ $(1—0)$
$(2—0)$ $(0—0)$ $(0—1)$ $(1—3)$ $(3—0)$
Now, how many similar arrangements are there of five dominoes that shall give six instead of five in the two additions?
Solutions: 1
This eBook is for the use of anyone anywhere in the United States and most other parts of the world at no cost and with almost no restrictions whatsoever. You may copy it, give it away or re-use it under the terms of the Project Gutenberg License included with this edition or online at http://www.gutenberg.org. If you are not located in the United States, you'll have to check the laws of the country where you are located before using this ebook.