(related to Problem: A War Puzzle Game)
The Britisher can always catch the enemy, no matter how clever and elusive that astute individual may be; but curious though it may seem, the British general can only do so after he has paid a somewhat mysterious visit to the particular town marked "$1$" in the map, going in by $3$ and leaving by $2,$ or entering by $2$ and leaving by $3.$ The three towns that are shaded and have no numbers do not really come into the question, as some may suppose, for the simple reason that the Britisher never needs to enter any one of them, while the enemy cannot be forced to go into them, and would be clearly ill-advised to do so voluntarily. We may, therefore, leave these out of consideration altogether. No matter what the enemy may do, the Britisher should make the following first nine moves: He should visit towns $24,$ $20,$ $19,$ $15,$ $11,$ $7,$ $3,$ $1,$ $2.$ If the enemy takes it into his head also to go to town $1,$ it will be found that he will have to beat a precipitate retreat the same way that he went in, or the Britisher will infallibly catch him in towns $2$ or $3,$ as the case may be. So the enemy will be wise to avoid that north-west corner of the map altogether.
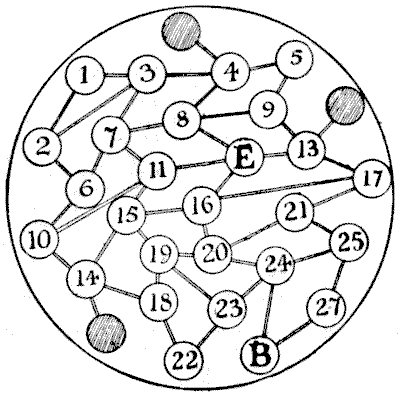
Now, when the British general has made the nine moves that I have given, the enemy will be, after his own ninth move, in one of the towns marked $5,$ $8,$ $11,$ $13,$ $14,$ $16,$ $19,$ $21,$ $24,$ or $27.$ Of course, if he imprudently goes to $3$ or $6$ at this point he will be caught at once. Wherever he may happen to be, the Britisher "goes for him," and has no longer any difficulty in catching him in eight more moves at most (seventeen in all) in one of the following ways. The Britisher will get to $8$ when the enemy is at $5,$ and win next move; or he will get to $19$ when the enemy is at $22,$ and win next move; or he will get to $24$ when the enemy is at $27,$ and so win next move. It will be found that he can be forced into one or other of these fatal positions.
In short, the strategy really amounts to this: the Britisher plays the first nine moves that I have given, and although the enemy does his very best to escape, our general goes after his antagonist and always driving him away from that north-west corner ultimately closes in with him, and wins. As I have said, the Britisher never need to make more than seventeen moves in all and may win in fewer moves if the enemy plays badly. But after playing those first nine moves it does not matter even if the Britisher makes a few bad ones. He may lose time, but cannot lose his advantage so long as he now keeps the enemy from town $1,$ and must eventually catch him.
This is a complete explanation of the puzzle. It may seem a little complex in print, but in practice, the winning play will now be quite easy to the reader. Make those nine moves, and there ought to be no difficulty whatever in finding the concluding line of play. Indeed, it might almost be said that then it is difficult for the British general not to catch the enemy. It is a question of what in chess we call the "opposition," and the visit by the Britisher to town $1$ "gives him the jump" on the enemy, as the man in the street would say.
Here is an illustrative example in which the enemy avoids capture as long as it is possible for him to do so. The Britisher's moves are above the line and the enemy's below it. Play them alternately. $$\begin{array}{rrrrrrrrrrrrrrrr} 24&20&19&15&11&7&3&1&2&6&10&14&18&19&20&24\\ \hline 13&9&13&17&21&20&24&23&19&15&19&23&24&25&27 \end{array}$$
The enemy must now go to $25$ or $B,$ in either of which towns he is immediately captured.
This eBook is for the use of anyone anywhere in the United States and most other parts of the world at no cost and with almost no restrictions whatsoever. You may copy it, give it away or re-use it under the terms of the Project Gutenberg License included with this edition or online at http://www.gutenberg.org. If you are not located in the United States, you'll have to check the laws of the country where you are located before using this ebook.