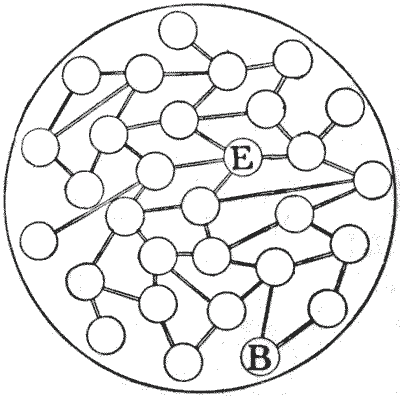
Here is another puzzle game. One player, representing the British general, places a counter at $B,$ and the other player, representing the enemy, places his counter at $E.$ The Britisher makes the first advance along one of the roads to the next town, then the enemy moves to one of his nearest towns, and so on in turns, until the British general gets into the same town as the enemy and captures him. Although each must always move along a road to the next town only, and the second player may do his utmost to avoid capture, the British general (as we should suppose, from the analogy of real life) must infallibly win. But how? That is the question.
Solutions: 1
This eBook is for the use of anyone anywhere in the United States and most other parts of the world at no cost and with almost no restrictions whatsoever. You may copy it, give it away or re-use it under the terms of the Project Gutenberg License included with this edition or online at http://www.gutenberg.org. If you are not located in the United States, you'll have to check the laws of the country where you are located before using this ebook.