"Look here," said the professor to his colleague, "I have been watching that fly on the octahedron, and it confines its walks entirely to the edges. What can be its reason for avoiding the sides?"
"Perhaps it is trying to solve some routing problem," suggested the other. "Supposing it to start from the top point, how many different routes are there by which it may walk over all the edges, without ever going twice along the same edge in any route?"
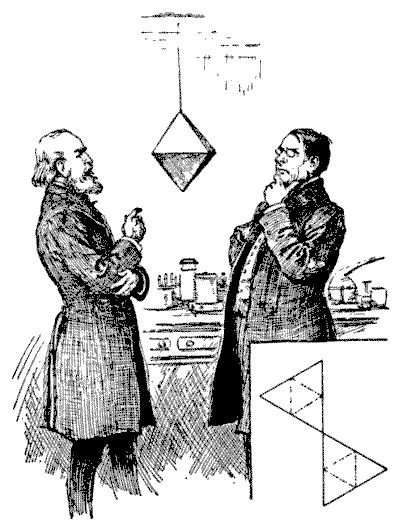
The problem was a harder one than they expected, and after working at it during leisure moments for several days their results did not agree—in fact, they were both wrong. If the reader is surprised at their failure, let him attempt the little puzzle himself. I will just explain that the octahedron is one of the five regular, or Platonic, bodies, and is contained under eight equal and equilateral triangles. If you cut out the two pieces of cardboard of the shape shown in the margin of the illustration, cut half through along the dotted lines and then bend them and put them together, you will have a perfect octahedron. In any route over all the edges, it will be found that the fly must end at the point of departure at the top.
Solutions: 1
This eBook is for the use of anyone anywhere in the United States and most other parts of the world at no cost and with almost no restrictions whatsoever. You may copy it, give it away or re-use it under the terms of the Project Gutenberg License included with this edition or online at http://www.gutenberg.org. If you are not located in the United States, you'll have to check the laws of the country where you are located before using this ebook.