(related to Problem: The Fly On The Octahedron)
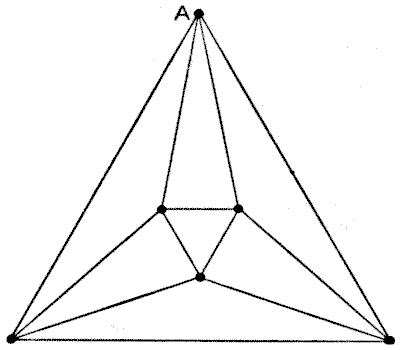
Though we cannot really see all the sides of the octahedron at once, we can make a projection of it that suits our purpose just as well. In the diagram, the six points represent the six angles of the octahedron, and four lines proceed from every point under exactly the same conditions as the twelve edges of the solid. Therefore if we start at the point $A$ and go over all the lines once, we must always end our route at $A.$ And the number of different routes is just $1,488,$ counting the reverse way of any route as different. It would take too much space to show how I make the count. It can be done in about five minutes, but an explanation of the method is difficult. The reader is therefore asked to accept my answer as correct.
This eBook is for the use of anyone anywhere in the United States and most other parts of the world at no cost and with almost no restrictions whatsoever. You may copy it, give it away or re-use it under the terms of the Project Gutenberg License included with this edition or online at http://www.gutenberg.org. If you are not located in the United States, you'll have to check the laws of the country where you are located before using this ebook.