(related to Problem: The Grand Tour)
The first thing to do in trying to solve a puzzle like this is to attempt to simplify it. If you look at Fig. $1,$ you will see that it is a simplified version of the map. Imagine the circular towns to be buttons and the railways to be connecting strings. (See solution to The Four Frogs) Then, it will be seen, we have simply "straightened out" the previous diagram without affecting the conditions. Now we can further simplify by converting Fig. $1$ into Fig. $2,$ which is a portion of a chessboard. Here the directions of the railways will resemble the moves of a rook in chess — that is, we may move in any direction parallel to the sides of the diagram, but not diagonally. Therefore the first town (or square) visited must be a black one; the second must be a white; the third must be a black; and so on. Every odd square visited will thus be black and every even one white. Now, we have $23$ squares to visit (an odd number), so the last square visited must be black. But $Z$ happens to be white, so the puzzle would seem to be impossible of solution.
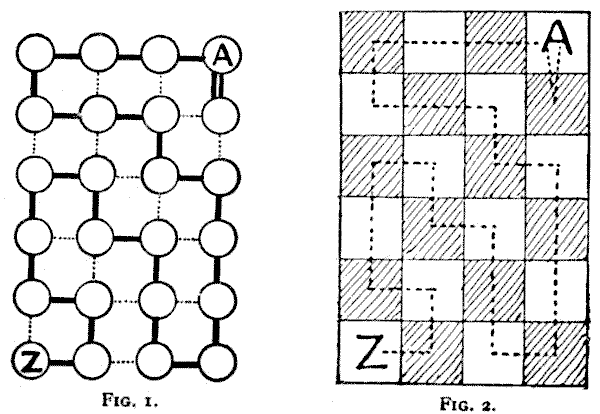
As we were told that the man "succeeded" in carrying put his plan, we must try to find some loophole in the conditions. He was to "enter every town once and only once," and we find no prohibition against his entering once the town $A$ after leaving it, especially as he has never left it since he was born, and would thus be "entering" it for the first time in his life. But he must return at once from the first town he visits, and then he will have only $22$ towns to visit, and as $22$ is an even number, there is no reason why he should not end on the white square $Z.$ A possible route for him is indicated by the dotted line from $A$ to $Z.$ This route is repeated by the dark lines in Fig. $1,$ and the reader will now have no difficulty in applying; it to the original map. We have thus proved that the puzzle can only be solved by a return to $A$ immediately after leaving it.
This eBook is for the use of anyone anywhere in the United States and most other parts of the world at no cost and with almost no restrictions whatsoever. You may copy it, give it away or re-use it under the terms of the Project Gutenberg License included with this edition or online at http://www.gutenberg.org. If you are not located in the United States, you'll have to check the laws of the country where you are located before using this ebook.