(related to Problem: The Sailor's Puzzle)
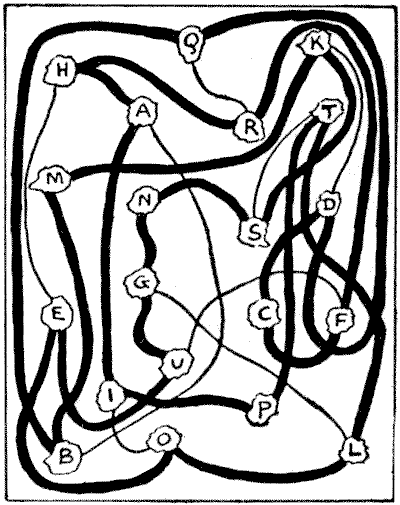
There are only four different routes (or eight, if we count the reverse ways) by which the sailor can start at the island marked $A,$ visit all the islands once, and once only, and return again to $A.$ Here they are:—
$$\begin{array}{c} A I P T L O E H R Q D C F U G N\\ S K M B A A I P T S N G L O E U\\ F C D K M B Q R H A A B M K S N\\ G L T P I O E U F C D Q R H A A I\\ P T L O E U G N S K M B Q D C F\\ R H A\end{array}$$
Now, if the sailor takes the first route he will make $C$ his 12th island (counting $A$ as $1$); by the second route he will make $C$ his 13th island; by the third route, his 16th island; and by the fourth route, his 17th island. If he goes the reverse way, $C$ will be respectively his 10th, 9th, 6th, and 5th island. As these are the only possible routes, it is evident that if the sailor puts off his visit to $C$ as long as possible, he must take the last route reading from left to right. This route I show by the dark lines in the diagram, and it is the correct answer to the puzzle.
The map may be greatly simplified by the "buttons and string" method, explained in the solution to The Four Frogs
This eBook is for the use of anyone anywhere in the United States and most other parts of the world at no cost and with almost no restrictions whatsoever. You may copy it, give it away or re-use it under the terms of the Project Gutenberg License included with this edition or online at http://www.gutenberg.org. If you are not located in the United States, you'll have to check the laws of the country where you are located before using this ebook.