◀ ▲ ▶Branches / Geometry / Elements-euclid / Book--3-circles / Definition: 3.04: Chords Equally Far From the Center of a Circle

Definition: 3.04: Chords Equally Far From the Center of a Circle

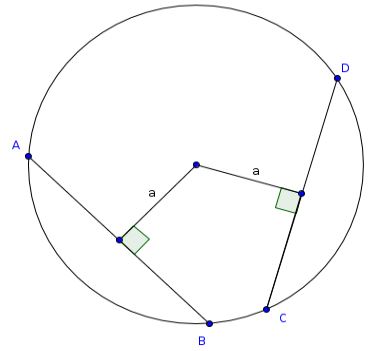
In a circle, straight lines are said to be equally far from the center when the perpendiculars drawn to them from the center are equal.

Modern Formulation

Chords are said to be equally distant from the center (or equally far from the center), if the perpendiculars constructed to them from the center are equal in length, i.e. congruent.

Example

In the following figure, the chords \(\overline{AB}\) and \(\overline{CD}\) are equally distant from the center, because the segments perpendicular to the chords have the same length \(a\) (i.e. they are congruent):

Mentioned in:

Proofs: 1 2
Propositions: 3 4

Thank you to the contributors under CC BY-SA 4.0!

Github:

non-Github:

@Calahan

@Fitzpatrick

References

Adapted from CC BY-SA 3.0 Sources:

1. Callahan, Daniel: "Euclid’s 'Elements' Redux" 2014

Adapted from (subject to copyright, with kind permission)

1. Fitzpatrick, Richard: Euclid's "Elements of Geometry"