Proposition: 3.37: Converse of Tangent Secant Theorem

(Proposition 37 from Book 3 of Euclid's “Elements”)

If some point is taken outside a circle, and two straight lines radiate from the point towards the circle, and one of them cuts the circle, and the (other) meets (it), and the (rectangle contained) by the whole (straight line) cutting (the circle), and the (part of it) cut off outside (the circle), between the point and the convex circumference, is equal to the (square) on the (straight line) meeting (the circle), then the (straight line) meeting (the circle) will touch the circle.

For let some point $D$ have been taken outside circle $ABC$, and let two straight lines, $DCA$ and $DB$, radiate from $D$ towards circle $ABC$, and let $DCA$ cut the circle, and let $DB$ meet (the circle).
And let the (rectangle contained) by $AD$ and $DC$ be equal to the (square) on $DB$.
I say that $DB$ touches circle $ABC$.

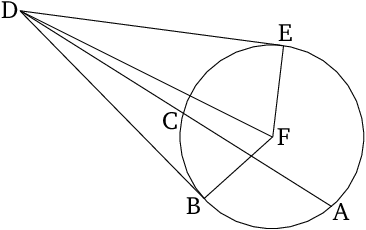
fig37e

Modern Formulation

If a straight line $DB$ intersects with a secant $DA$ of a given circle in $D$ and this secant cuts the circle at the points $C$ and $A$ such that for the lengths segments fulfill the inequality $|\overline{DC}|<|\overline{DA}|$, and if $|\overline{DC}|\cdot |\overline{DA}|=|\overline{DB}|^2,$ then $DB$ is a tangent $DB$ touching the circle at $D.$

Proofs: 1

Proofs: 1
Sections: 2

Thank you to the contributors under CC BY-SA 4.0!