Proposition: 7.06: Division with Quotient and Remainder Obeys Distributive Law (Sum)

(Proposition 6 from Book 7 of Euclid's “Elements”)

If a number is parts of a number, and another (number) is the same parts of another, then the sum (of the leading numbers) will also be the same parts of the sum (of the following numbers) that one (number) is of another.

For let a number $AB$ be parts of a number $C$, and another (number) $DE$ (be) the same parts of another (number) $F$ that $AB$ (is) of $C$.
I say that the sum $AB$, $DE$ is also the same parts of the sum $C$, $F$ that $AB$ (is) of $C$.

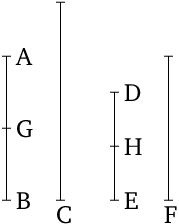
fig06e

Modern Formulation

See divisibility law no. 9.

Notes

This proposition states (for integers $0 < r_0 < AG$ and $0 < r_1 < DH$) $$\begin{array}{rclclc}C&=&AB+r_0&=&n\cdot AG+r_0&\wedge\\ F&=&DE+r_1&=&n\cdot DH+r_1\\ &\Downarrow&\\ C+F&=&(AB+DE)+(r_0+r_1)&=&n(AG+DH)+(r_0+r_1) \end{array}$$

with $0 < (r_0+r_1) < (AG+DH).$ In particular,

$$n\not\mid (C+F)\Rightarrow n\not\mid C\vee n\not\mid F.$$

Proofs: 1

Proofs: 1 2 3

Thank you to the contributors under CC BY-SA 4.0!