Proof: By Euclid
(related to Proposition: Prop. 10.017: Condition for Commensurability of Roots of Quadratic Equation)
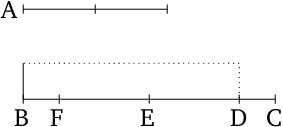
- For let $BC$ have been cut in half at the point $E$ [Prop. 1.10].
- And let $EF$ be made equal to $DE$ [Prop. 1.3].
- Thus, the remainder $DC$ is equal to $BF$.
- And since the straight line $BC$ has been cut into equal (pieces) at $E$, and into unequal (pieces) at $D$, the rectangle contained by $BD$ and $DC$, plus the square on $ED$, is thus equal to the square on $EC$ [Prop. 2.5].
- (The same) also (for) the quadruples.
- Thus, four times the (rectangle contained) by $BD$ and $DC$, plus the quadruple of the (square) on $DE$, is equal to four times the square on $EC$.
- But, the square on $A$ is equal to the quadruple of the (rectangle contained) by $BD$ and $DC$, and the square on $DF$ is equal to the quadruple of the (square) on $DE$.
- For $DF$ is double $DE$.
- And the square on $BC$ is equal to the quadruple of the (square) on $EC$.
- For, again, $BC$ is double $CE$.
- Thus, the (sum of the) squares on $A$ and $DF$ is equal to the square on $BC$.
- Hence, the (square) on $BC$ is greater than the (square) on $A$ by the (square) on $DF$.
- Thus, $BC$ is greater in square than $A$ by $DF$.
- It must also be shown that $BC$ is commensurable (in length) with $DF$.
- For since $BD$ is commensurable in length with $DC$, $BC$ is thus also commensurable in length with $CD$ [Prop. 10.15].
- But, $CD$ is commensurable in length with $CD$ plus $BF$.
- For $CD$ is equal to $BF$ [Prop. 10.6].
- Thus, $BC$ is also commensurable in length with $BF$ plus $CD$ [Prop. 10.12].
- Hence, $BC$ is also commensurable in length with the remainder $FD$ [Prop. 10.15].
- Thus, the square on $BC$ is greater than (the square on) $A$ by the (square) on (some straight line) commensurable (in length) with ($BC$).
- And so let the square on $BC$ be greater than the (square on) $A$ by the (square) on (some straight line) commensurable (in length) with ($BC$).
- And let a (rectangle) equal to the fourth (part) of the (square) on $A$, falling short by a square figure, have been applied to $BC$.
- And let it be the (rectangle contained) by $BD$ and $DC$.
- It must be shown that $BD$ is commensurable in length with $DC$.
- For, similarly, by the same construction, we can show that the square on $BC$ is greater than the (square on) $A$ by the (square) on $FD$.
- And the square on $BC$ is greater than the (square on) $A$ by the (square) on (some straight line) commensurable (in length) with ($BC$).
- Thus, $BC$ is commensurable in length with $FD$.
- Hence, $BC$ is also commensurable in length with the remaining sum of $BF$ and $DC$ [Prop. 10.15].
- But, the sum of $BF$ and $DC$ is commensurable [in length] with $DC$ [Prop. 10.6].
- Hence, $BC$ is also commensurable in length with $CD$ [Prop. 10.12].
- Thus, via separation, $BD$ is also commensurable in length with $DC$ [Prop. 10.15].
- Thus, if there are two unequal straight lines, and so on ....
∎
Thank you to the contributors under CC BY-SA 4.0! 

- Github:
-

- non-Github:
- @Fitzpatrick
References
Adapted from (subject to copyright, with kind permission)
- Fitzpatrick, Richard: Euclid's "Elements of Geometry"
