◀ ▲ ▶Branches / Geometry / Elements-euclid / Book-12-proportional-stereometry / Proof: By Euclid

Proof: By Euclid

(related to Proposition: Prop. 12.10: Volume of Cone is Third of Cylinder on Same Base and of Same Height)

• For let there be a cone (with) the same base as a cylinder, (namely) the circle $ABCD$, and an equal height.
• I say that the cone is the third part of the cylinder - that is to say, that the cylinder is three times the cone.

• For if the cylinder is not three times the cone then the cylinder will be either more than three times, or less than three times, (the cone).
• Let it, first of all, be more than three times (the cone).
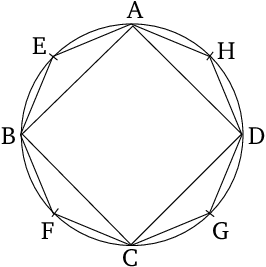
• And let the square $ABCD$ have been inscribed in circle $ABCD$ [Prop. 4.6].
• So, square $ABCD$ is more than half of circle $ABCD$ [Prop. 12.2].
• And let a prism of equal height to the cylinder have been set up on square $ABCD$.
• So, the prism set up is more than half of the cylinder, inasmuch as if we also circumscribe a square around circle $ABCD$ [Prop. 4.7] then the square inscribed in circle $ABCD$ is half of the circumscribed (square).
• And the solids set up on them are parallelepiped prisms of equal height.
• And parallelepiped solids having the same height are to one another as their bases [Prop. 11.32].
• And, thus, the prism set up on square $ABCD$ is half of the prism set up on the square circumscribed about circle $ABCD$.
• And the cylinder is less than the prism set up on the square circumscribed about circle $ABCD$.
• Thus, the prism set up on square $ABCD$ of the same height as the cylinder is more than half of the cylinder.
• Let the circumferences $AB$, $BC$, $CD$, and $DA$ have been cut in half at points $E$, $F$, $G$, and $H$.
• And let $AE$, $EB$, $BF$, $FC$, $CG$, $GD$, $DH$, and $HA$ have been joined.
• And thus each of the triangles $AEB$, $BFC$, $CGD$, and $DHA$ is more than half of the segment of circle $ABCD$ about it, as was shown previously [Prop. 12.2].
• Let prisms of equal height to the cylinder have been set up on each of the triangles $AEB$, $BFC$, $CGD$, and $DHA$.
• And each of the prisms set up is greater than the half part of the segment of the cylinder about it - inasmuch as if we draw (straight lines) parallel to $AB$, $BC$, $CD$, and $DA$ through points $E$, $F$, $G$, and $H$ (respectively), and complete the parallelograms on $AB$, $BC$, $CD$, and $DA$, and set up parallelepiped solids of equal height to the cylinder on them, then the prisms on triangles $AEB$, $BFC$, $CGD$, and $DHA$ are each half of the set up (parallelepipeds).
• And the segments of the cylinder are less than the set up parallelepiped solids.
• Hence, the prisms on triangles $AEB$, $BFC$, $CGD$, and $DHA$ are also greater than half of the segments of the cylinder about them.
• So (if) the remaining circumferences are cut in half, and straight lines are joined, and prisms of equal height to the cylinder are set up on each of the triangles, and this is done continually, then we will (eventually) leave some segments of the cylinder whose (sum) is less than the excess by which the cylinder exceeds three times the cone [Prop. 10.1].
• Let them have been left, and let them be $AE$, $EB$, $BF$, $FC$, $CG$, $GD$, $DH$, and $HA$.
• Thus, the remaining prism whose base (is) polygon $AEBFCGDH$, and height the same as the cylinder, is greater than three times the cone.
• But, the prism whose base is polygon $AEBFCGDH$, and height the same as the cylinder, is three times the pyramid whose base is polygon $AEBFCGDH$, and apex the same as the cone [Prop. 12.7 corr.] .
• And thus the pyramid whose base [is] [polygon]bookofproofs$687 $AEBFCGDH$, and apex the same as the cone, is greater than the cone having (as) base circle $ABCD$.
• But (it is) also less.
• For it is encompassed by it.
• The very thing (is) impossible.
• Thus, the cylinder is not more than three times the cone.
• So, I say that neither (is) the cylinder less than three times the cone.
• For, if possible, let the cylinder be less than three times the cone.
• Thus, inversely, the cone is greater than the third part of the cylinder.
• So, let the square $ABCD$ have been inscribed in circle $ABCD$ [Prop. 4.6].
• Thus, square $ABCD$ is greater than half of circle $ABCD$.
• And let a pyramid having the same apex as the cone have been set up on square $ABCD$.
• Thus, the pyramid set up is greater than the half part of the cone, inasmuch as we showed previously that if we circumscribe a square about the circle [Prop. 4.7] then the square $ABCD$ will be half of the square circumscribed about the circle [Prop. 12.2].
• And if we set up on the squares parallelepiped solids - which are also called prisms - of the same height as the cone, then the (prism) set up on square $ABCD$ will be half of the (prism) set up on the square circumscribed about the circle.
• For they are to one another as their bases [Prop. 11.32].
• Hence, (the same) also (goes for) the thirds.
• Thus, the pyramid whose base is square $ABCD$ is half of the pyramid set up on the square circumscribed about the circle [Prop. 12.7 corr.] .
• And the pyramid set up on the square circumscribed about the circle is greater than the cone.
• For it encompasses it.
• Thus, the pyramid whose base is square $ABCD$, and apex the same as the cone, is greater than half of the cone.
• Let the circumferences $AB$, $BC$, $CD$, and $DA$ have been cut in half at points $E$, $F$, $G$, and $H$ (respectively).
• And let $AE$, $EB$, $BF$, $FC$, $CG$, $GD$, $DH$, and $HA$ have been joined.
• And, thus, each of the triangles $AEB$, $BFC$, $CGD$, and $DHA$ is greater than the half part of the segment of circle $ABCD$ about it [Prop. 12.2].
• And let pyramids having the same apex as the cone have been set up on each of the triangles $AEB$, $BFC$, $CGD$, and $DHA$.
• And, thus, in the same way, each of the pyramids set up is more than the half part of the segment of the cone about it.
• So, (if) the remaining circumferences are cut in half, and straight lines are joined, and pyramids having the same apex as the cone are set up on each of the triangles, and this is done continually, then we will (eventually) leave some segments of the cone whose (sum) is less than the excess by which the cone exceeds the third part of the cylinder [Prop. 10.1].
• Let them have been left, and let them be the (segments) on $AE$, $EB$, $BF$, $FC$, $CG$, $GD$, $DH$, and $HA$.
• Thus, the remaining pyramid whose base is polygon $AEBFCGDH$, and apex the same as the cone, is greater than the third part of the cylinder.
• But, the pyramid whose base is polygon $AEBFCGDH$, and apex the same as the cone, is the third part of the prism whose base is polygon $AEBFCGDH$, and height the same as the cylinder [Prop. 12.7 corr.] .
• Thus, the prism whose base is polygon $AEBFCGDH$, and height the same as the cylinder, is greater than the cylinder whose base is circle $ABCD$.
• But, (it is) also less.
• For it is encompassed by it.
• The very thing is impossible.
• Thus, the cylinder is not less than three times the cone.
• And it was shown that neither (is it) greater than three times (the cone).
• Thus, the cylinder (is) three times the cone.
• Hence, the cone is the third part of the cylinder.
• Thus, every cone is the third part of the cylinder which has the same base as it, and an equal height.
• (Which is) the very thing it was required to show.
  ∎

Thank you to the contributors under CC BY-SA 4.0!

Github:

non-Github:

@Fitzpatrick

References

Adapted from (subject to copyright, with kind permission)

1. Fitzpatrick, Richard: Euclid's "Elements of Geometry"