◀ ▲ ▶Branches / Geometry / Elements-euclid / Book-13-platonic-solids / Proposition: Prop. 13.09: Sides Appended of Hexagon and Decagon inscribed in same Circle are cut in Extreme and Mean Ratio

Proposition: Prop. 13.09: Sides Appended of Hexagon and Decagon inscribed in same Circle are cut in Extreme and Mean Ratio

(Proposition 9 from Book 13 of Euclid's “Elements”)

If the side of a hexagon and of a decagon inscribed in the same circle are added together then the whole straight line has been cut in extreme and mean ratio (at the junction point), and its greater piece is the side of the hexagon.

• Let $ABC$ be a circle.
• And of the figures inscribed in circle $ABC$, let $BC$ be the side of a decagon, and $CD$ (the side) of a hexagon.
• And let them be (laid down) straight-on (to one another).
• I say that the whole straight line $BD$ has been cut in extreme and mean ratio (at $C$), and that $CD$ is its greater piece.

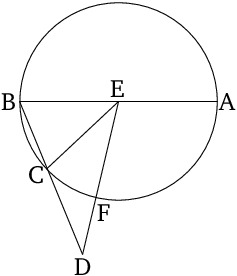
Modern Formulation

If the circle is of unit radius then the side of the hexagon is 1, whereas the side of the decagon is \[\frac {\sqrt{5}-1}2.\]

Table of Contents

Proofs: 1

Mentioned in:

Proofs: 1 2

Thank you to the contributors under CC BY-SA 4.0!

Github:

non-Github:

@Fitzpatrick

References

Adapted from (subject to copyright, with kind permission)

1. Fitzpatrick, Richard: Euclid's "Elements of Geometry"

Adapted from CC BY-SA 3.0 Sources:

1. Prime.mover and others: "Pr∞fWiki", https://proofwiki.org/wiki/Main_Page, 2016