A straight line is said to have been cut in extreme and mean ratio when as the whole is to the greater segment so the greater (segment is) to the lesser.
A segment with the length $a+b$ is cut in inverse golden ratio if $$\phi:=\frac{a+b}b=\frac ba.$$
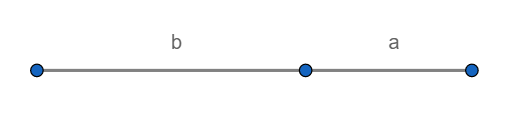
It is possible to determine that this ratio must be $$\phi=\frac{\sqrt 5-1}{2}=0.61803398875\ldots$$
This number is the inverse of the golden ratio $$\Phi:=\frac{1}{\phi}=\frac{\sqrt 5+1}{2}=1.61803398875\ldots$$
Corollaries: 1
Proofs: 2 3 4 5 6 7 8 9 10 11 12 13 14
Propositions: 15 16 17 18 19 20 21 22 23 24