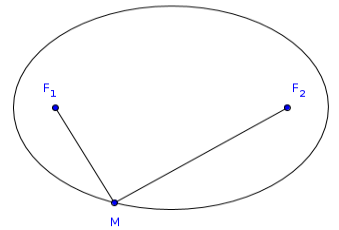
Let \(F_1\) and \(F_2\) be two fixed points in a plane \(\mathcal P\). An ellipse is the plane figure comprised of the set of points \(M\in\mathcal P\) such that the sum of their lengths of the segments to \(\overline{MF_1}\) and \(\overline{MF_2}\) is constant. \(F_1\) and \(F_2\) are called the focal points of the ellipse.
\[d(M,F_1)+d(M,F_2)=\operatorname{const.}\]
(c) bookofproofs