(related to Algorithm: Get the Cut Vertices and Biconnected Components of a Connected Graph)
We only provide a sketch of a proof:
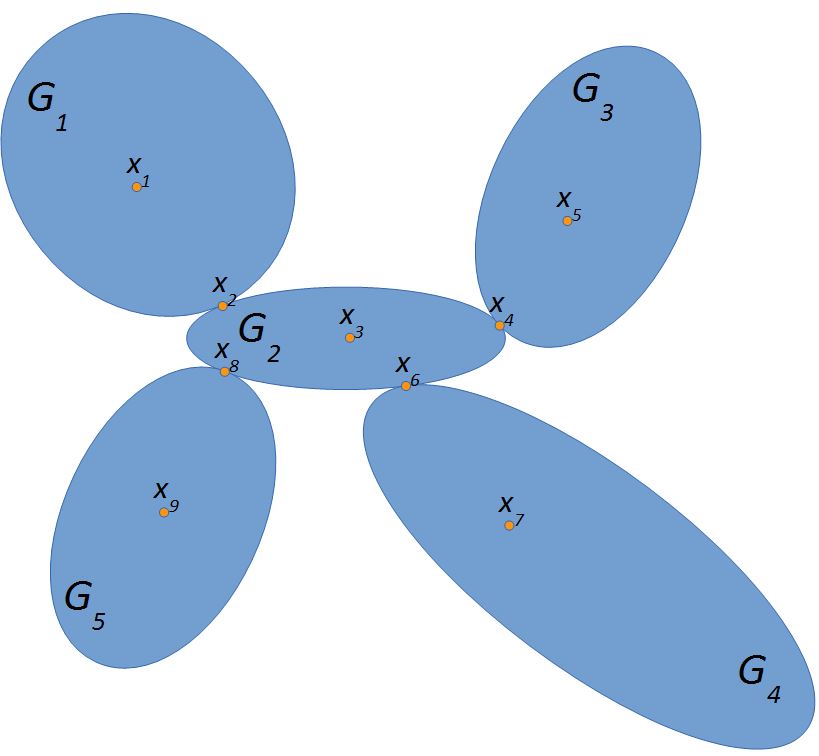
The central idea of the proof can be understood by studying the example in the next figure, which shows schematically a connected graph with \(5\) biconnected components \(G_1,G_2,G_3,G_4\) and \(G_5\). The vertices \(x_2,x_4,x_6,x_8\) are cutvertices.
Imagine, we start the depth-first search (DFS) at, say, some vertex \(x_1\) in \(G_1\) and pass to a vertex \(x_3\) in \(G_2\) through the cutvertex \(x_2\). We might then leave \(G_2\) through the cutvertex \(x_4\) and reach the vertex \(x_5\) in \(G_3\). By the nature of the DFS, all the vertices of \(G_3\) must be traversed, before we come back to the cutvertex \(x_4\). Thus, \(G_3\) consists of exactly those vertices, which are connected to the neighbors of the cutvertex \(x_4\) in \(G_3\) such that they have been visited after the vertex \(x_4\). The check, if these neighbors have been visited after \(x_4\), is done by calculating the so-called lowpoint (see IF-command in the lines \(36 - 38\) of the algorithm).
Matters get a little more complicated, if we re-enter \(G_2\) and, without traversing it completely, enter the biconnected component \(G_4\). Like \(G_3\) before, \(G_4\) this is a dead end and we have to traverse it completely, before again reentering \(G_2\) (after identifying \(G_4\) as a biconnected component and \(x_6\) as its cutvertex.
Fortunately, because we store all visited vertices in a stack, it does not matter, if we leave again \(G_2\) without traversing it completely. By the time we have found the last biconnected component (here \(G_5\)), we will finally traverse \(G_2\) completely, returning back to the cutvertex \(x_2\).
The method described above works pretty well for almost every starting vertex \(x_1\) (root of the DFS), if it is not a cutvertex, where we would fail to identify the cutvertex properly. However, for this special case, the first vertex is cutvertex, if and only if it has two or more descendants, i.e. points in the DFS, where we have to pass through this vertex to visit more biconnected components.