◀ ▲ ▶Branches / Number-theory / Sieve-methods / Lemma: Sieve for Twin Primes

It is well-known that using the sieve of Eratosthenes, we can generate the sequence of primes $2,3,5,7,11,13,17,19,\ldots\), which is known to be infinite. It is a longstanding problem to prove if there are (or there are not) infinitely many twin primes \((3,5),~(5,7),~(11,13),~(17,19),~(29,31),\ldots\).

There exists an efficient method[^6913] to sieve all twin primes of the form \((6k-1,6k+1)\), \(k=1,2,\ldots\).

Note that these are all twin primes except the twin primes \((3,5)\). This is because even almost all primes (and not only twin primes) can be written in this form¹.

A Sieve for Twin Primes and the Twin Prime Sequence

1. Start with the sequence of positive natural numbers \(1,2,3,4,\ldots\).
2. Use the known infinite sequence of primes \(p > 3\), i.e. the primes \(5, 7, 11, 13,17, 19, 23, 29,\ldots\) in the following way:

1. Set the number \(f_p\) to the value of the floor function \(f_p:=\lfloor (p+1)/6\rfloor\).

1. Sieve from the above sequence of all positive natural numbers the numbers \(pk-f_p\) and \(pk+f_p\) for \(k=1,2,3,\ldots\).

1. Repeat this procedure for all primes \(p > 3\).

1. The remaining sequence starts with \(k=1, 2, 3, 5, 7, 10, 12, 17, 18, 23, 25, 30, 32, 33,\ldots\).
2. The twin primes can be restored from this remaining sequence as follows:

1. Build pairs of numbers \((6k-1,6k+1)\) for \(k=1, 2, 3, 5, 7, 10, 12, 17, 18, 23, 25, 30, 32, 33,\ldots\).

1. These pairs are all twin primes, except \((3,5)\), i.e. the twin primes \((5,7),~(11,13),~(17,19),~(29,31),~(41,43),\ldots\).

The following figure visualizes this sieve method:

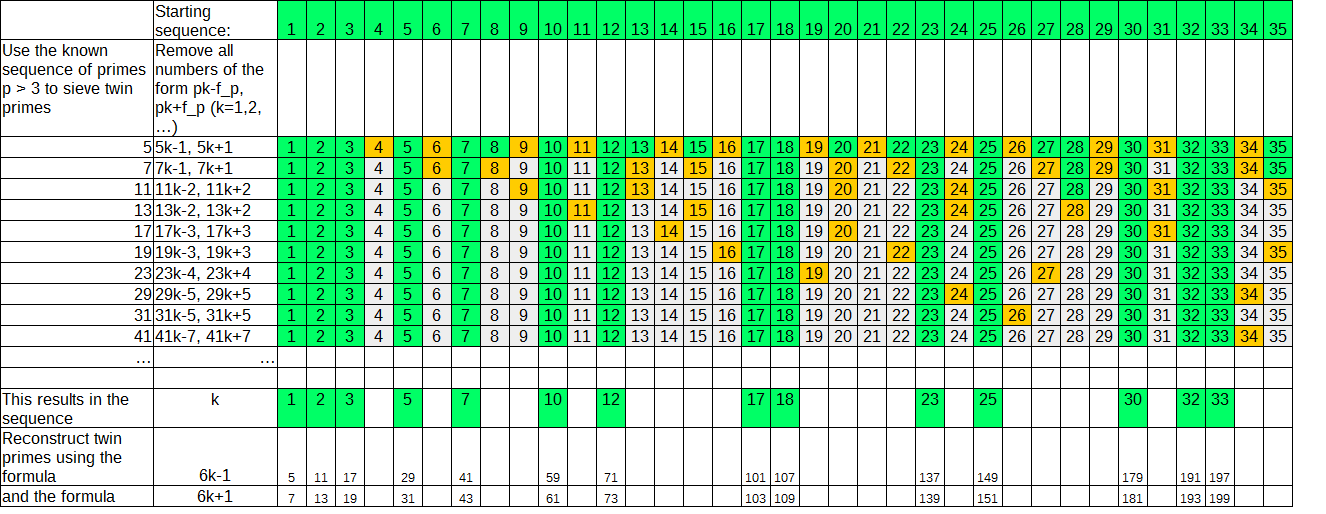
With this respect, the sequence \(k=1, 2, 3, 5, 7, 10, 12, 17, 18, 23, 25, 30, 32, 33,\ldots\) can be called the twin prime sequence.

The following lemma formalizes this result.

Lemma: Sieve for Twin Primes

Let $n\ge 1$ be an integer. The integer $a_n:=36n^2-1$ is the product of two twin primes $p=6n-1$ and $q=6n+1$ if and only if $n\not\equiv\pm f_s\mod s$ for all primes $s$ with $5\le s\le\sqrt q,$ where, using the floor function, the residue classes $f_s$ are defined by $$f_s:=\left\lfloor\frac {s+1}6\right\rfloor.$$