◀ ▲ ▶Branches / Topology / Definition: Topological Product, Product Topology
Definition: Topological Product, Product Topology
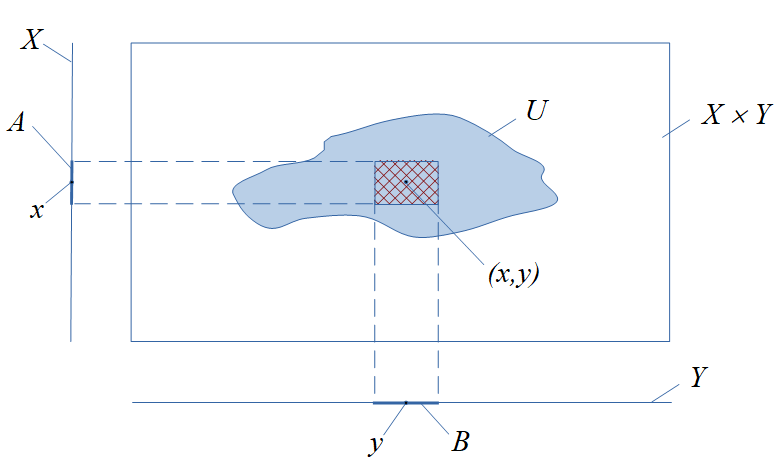
Let $(X,\mathcal O_X)$ and $(Y,\mathcal O_Y)$ be two topological spaces. The topological product (or product space) $(Z,\mathcal O_Z)$ of $X$ and $Y$ is defined as $$ (Z,\mathcal O_Z):=(X\times Y,\mathcal O_Z\},$$ where $X\times Y$ denotes the usual Cartesian product.

The product topology $\mathcal O_Z$ of the topological product is defined as a set of subsets $U\subseteq X\times Y$ such that for every $(x,y)\in U\in\mathcal O_Z$ there exist open sets $A\in\mathcal O_X$ and $B\in\mathcal O_Y$ such that $x\in A,$ $y\in B,$ and $A\times B\subset U.$
Notes
- The Cartesian product $A\times B$ is also called an open box.
- The product topology is the coarsest topology on $Z$ such that all of the coordinate projection are continuous. This topology is called the Tychonoff topology.
Mentioned in:
Definitions: 1
Thank you to the contributors under CC BY-SA 4.0! 

- Github:
-

References
Bibliography
- Steen, L.A.;Seebach J.A.Jr.: "Counterexamples in Topology", Dover Publications, Inc, 1970
- Jänich, Klaus: "Topologie", Springer, 2001, 7th Edition

