Let \(M\) be a manifold and let \(U_{\alpha},U_{\beta}\subseteq M\) be its open subsets. Furthermore, let \(V_\alpha,V_\beta\subseteq\mathbb R^{n}\) be open subsets of the \(n\)-dimensional metric space or real numbers \(\mathbb {R} ^{n}\).
Consider two topological charts \(\varphi_{\alpha}\colon U_{\alpha}\rightarrow V_{\alpha}\) and \(\varphi_{\beta}\colon U_{\beta}\rightarrow V_{\beta}\). Then we call a composition of the homeomorphisms. \[\tau_{\alpha,\beta}:=\varphi_{\beta}\circ \varphi_{\alpha}^{-1}=V_{\alpha}\cap \varphi_{\alpha}(U_{\alpha}\cap U_{\beta})\longrightarrow V_{\beta}\cap \varphi_{\beta}(U_{\alpha}\cap U_{\beta}) \]
the transition map of the topological charts.
Note that since \(\varphi _{\alpha }\) and \(\varphi _{\beta }\) are both homeomorphisms, the transition map \(\tau _{\alpha ,\beta }\) is also a homeomorphism.
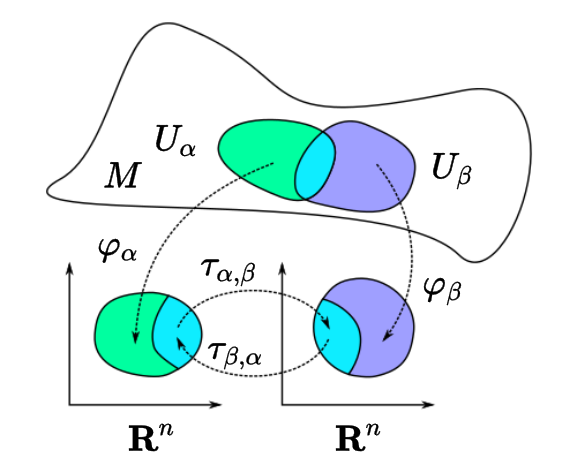
(picture by Stomatapoll, wikipedia)
Definitions: 1