(related to Section: Uniform Convergence of Functions)
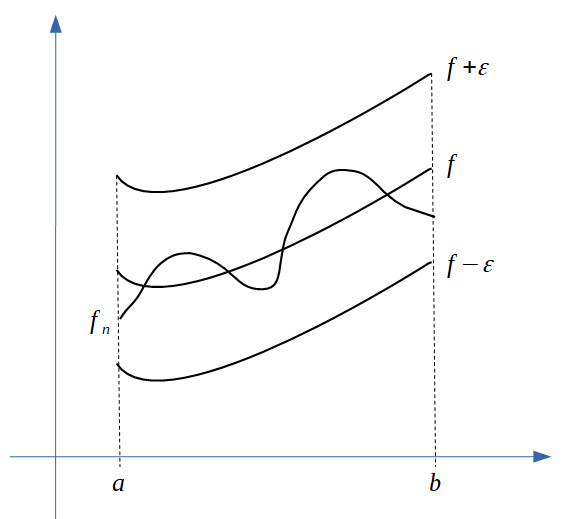
The concept of uniformly convergent functions can be better understood when thinking of the sequence members $f_n:[a,b]\to\mathbb R$ as having all values $x\in[a,b]$ inside an $\epsilon$-strip above and below the limit function $f:[a,b]\to\mathbb R,$ no matter how small $\epsilon > 0$ is chosen, as illustrated in the following figure:
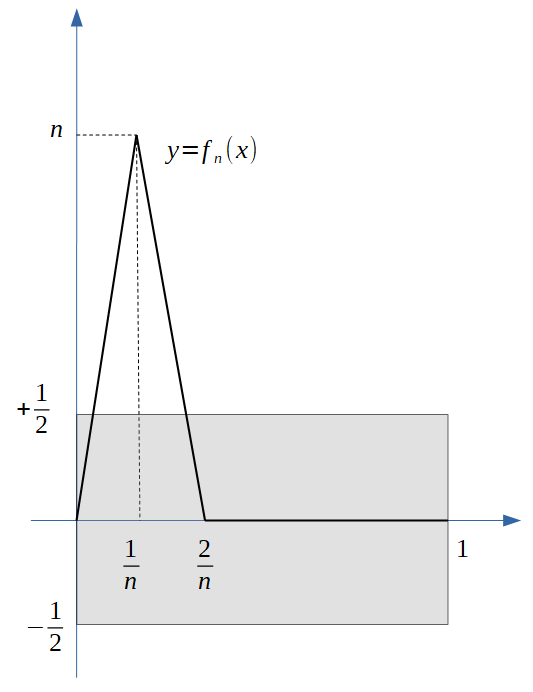
If, for a given $\epsilon >0$ there is at least one $x\in[a,b]$ for which the functions $f_n$ exceed the $\epsilon$-strip, the functions are not uniformly convergent functions, however, they still can converge to the limit function pointwise. The following sequence of functions is an example of a pointwise but not uniformly convergent sequence of functions.
For $n\ge 2$ we define the functions $f_n:[0,1]\to\mathbb R$ by
$$f_n(x):=\max\left(n-n^2\cdot\left|x-\frac 1n\right|,0\right).$$
Note that for $x=0$ we have $f_n(x)=0$ for all $n \ge 2.$ On the other hand, if $x\in(0,1]$, then we can find an index $N\ge 2$ such that $\frac 2n\le x$ for all $n\ge N.$ In other words, $$\lim_{n\to\infty}f_n(x)=0\quad\forall x\in[0,1],$$ which means that this sequence of functions is pointwise convergent to the constant limit function $f(x)=0.$ for all $x\in[0,1].$
However, the sequence does not converge uniformly to this limit function. For no $n\ge n$ we have $$|f_n(x)-0|<1\quad\forall x\in[0,1].$$ If it doesn't for $\epsilon = 1$, it certainly doesn't if we choose $\epsilon > 0$ even smaller. This behavior can be also seen in the following figure: