The puzzle of making a complete tour of the chessboard with the queen in the fewest possible moves (in which squares may be visited more than once) was first given by the late Sam Loyd in his Chess Strategy. But the solution shown below is the one he gave in American Chess-Nuts in 1868. I have recorded at least six different solutions in the minimum number of moves—fourteen—but this one is the best of all, for reasons I will explain.
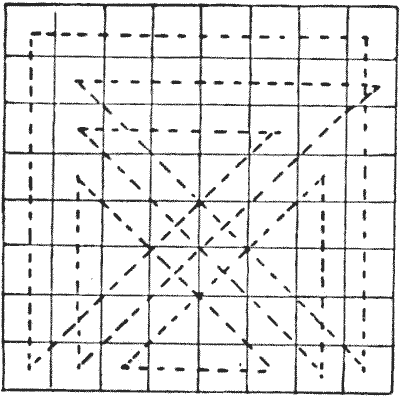
If you will look at the lettered square you will understand that there are only ten really differently placed squares on a chessboard—those enclosed by a dark line—all the others are mere reversals or reflections. For example, every A is a corner square, and every J a central square. Consequently, as the solution shown has a turning-point at the enclosed D square, we can obtain a solution starting from and ending at any square marked $D$ — by just turning the board about. Now, this scheme will give you a tour starting from any $A, B, C, D, E, F,$ or $H,$ while no other route that I know can be adapted to more than five different starting-points. There is no Queen's Tour in fourteen moves (remember a tour must be re-entrant) that may start from a $G, I,$ or $J.$ But we can have a non-re-entrant path over the whole board in fourteen moves, starting from any given square. Hence the following puzzle:—
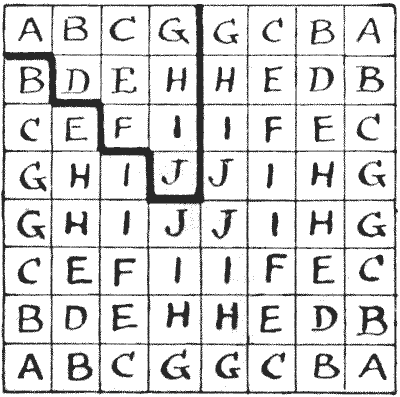
Start from the $J$ in the enclosed part of the lettered diagram and visit every square of the board in fourteen moves, ending wherever you like.
Solutions: 1
This eBook is for the use of anyone anywhere in the United States and most other parts of the world at no cost and with almost no restrictions whatsoever. You may copy it, give it away or re-use it under the terms of the Project Gutenberg License included with this edition or online at http://www.gutenberg.org. If you are not located in the United States, you'll have to check the laws of the country where you are located before using this ebook.