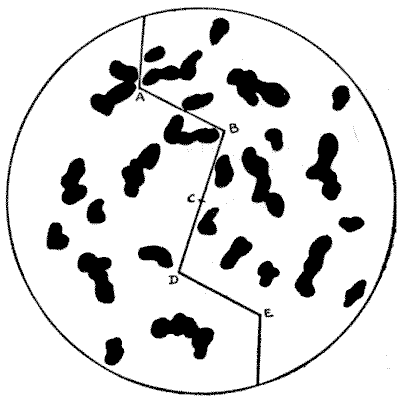
(related to Problem: The Christmas Pudding)
The illustration shows how the pudding may be cut into two parts of exactly the same size and shape. The lines must necessarily pass through the points $A, B, C, D,$ and $E.$ But, subject to this condition, they may be varied in an infinite number of ways. For example, at a point midway between $A$ and the edge, the line may be completed in an unlimited number of ways (straight or crooked), provided it be exactly reflected from $E$ to the opposite edge. And similar variations may be introduced at other places.
This eBook is for the use of anyone anywhere in the United States and most other parts of the world at no cost and with almost no restrictions whatsoever. You may copy it, give it away or re-use it under the terms of the Project Gutenberg License included with this edition or online at http://www.gutenberg.org. If you are not located in the United States, you'll have to check the laws of the country where you are located before using this ebook.