(related to Problem: The Pentagon and Square)
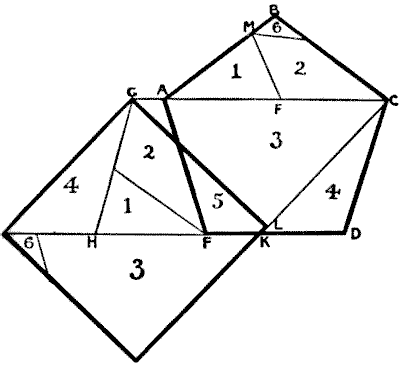
A regular pentagon may be cut into as few as six pieces that will fit together without any turning over and form a square, as I shall show below. Hitherto the best answer has been in seven pieces — the solution produced some years ago by a foreign mathematician, Paul Busschop. We first form a parallelogram, and from that the square. The process will be seen in the diagram on the next page.
The pentagon is $ABCDE.$ By the cut $AC$ and the cut $FM$ ($F$ being the middle point between $A$ and $C,$ and $M$ being the same distance from $A$ as $F$) we get two pieces that may be placed in position at $GHEA$ and form the parallelogram $GHDC.$ We then find the mean proportional between the length $HD$ and the height of the parallelogram. This distance we mark off from $C$ at $K,$ then draw $CK,$ and from $G$ drop the line $GL,$ perpendicular to $KC.$ The rest is easy and rather obvious. It will be seen that the six pieces will form either the pentagon or the square.
I have received what purported to be a solution in five pieces, but the method was based on the rather subtle fallacy that half the diagonal plus half the side of a pentagon equals the side of a square of the same area. I say subtle, because it is an extremely close approximation that will deceive the eye, and is quite difficult to prove inexact. I am not aware that attention has before been drawn to this curious approximation.
Another correspondent made the side of his square $1\frac 14$ of the side of the pentagon. As a matter of fact, the ratio is irrational. I calculate that if the side of the pentagon is $1$ — inch, foot, or anything else — the side of the square of equal area is $1.3117$ nearly, or say roughly $1\frac{3}{10}$. So we can only hope to solve the puzzle by geometrical methods.
This eBook is for the use of anyone anywhere in the United States and most other parts of the world at no cost and with almost no restrictions whatsoever. You may copy it, give it away or re-use it under the terms of the Project Gutenberg License included with this edition or online at http://www.gutenberg.org. If you are not located in the United States, you'll have to check the laws of the country where you are located before using this ebook.