I wonder how many of my readers, amongst those who have not given any close attention to the elements of geometry, could draw a regular pentagon, or five-sided figure, if they suddenly required to do so. A regular hexagon, or six-sided figure, is easy enough, for everybody knows that all you have to do is to describe a circle and then, taking the radius as the length of one of the sides, mark off the six points round the circumference. But a pentagon is quite another matter.
So, as my puzzle has to do with the cutting up of a regular pentagon, it will perhaps be well if I first show my less experienced readers how this figure is to be correctly drawn. Describe a circle and draw the two lines $H B$ and $D G$, in the diagram, through the center at right angles Now find the point $A,$ midway between $C$ and $B.$1 Next place the point of your compasses at $A$ and with the distance $A D$ describe the arc cutting $H B$ at $E.$ Then place the point of your compasses at $D$ and with the distance $D E$ describe the arc cutting the circumference at $F.$ Now, $D F$ is one of the sides of your pentagon, and you have simply to mark off the other sides round the circle. Quite simple when you know how, but otherwise somewhat of a poser.
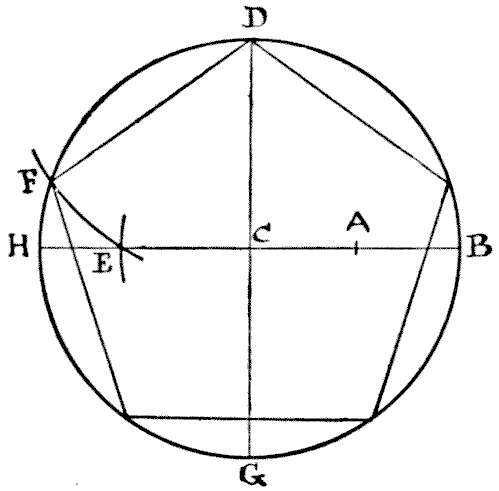
Having formed your pentagon, the puzzle is to cut it into the fewest possible pieces that will fit together and form a perfect square
Solutions: 1
This eBook is for the use of anyone anywhere in the United States and most other parts of the world at no cost and with almost no restrictions whatsoever. You may copy it, give it away or re-use it under the terms of the Project Gutenberg License included with this edition or online at http://www.gutenberg.org. If you are not located in the United States, you'll have to check the laws of the country where you are located before using this ebook.
(editor's remark: see how to bisect a segment). ↩