A speculative country builder has a circular field, on which he has erected four cottages, as shown in the illustration. The field is surrounded by a brick wall, and the owner undertook to put up three other brick walls, so that the neighbours should not be overlooked by each other, but the four tenants insist that there shall be no favouritism and that each shall have exactly the same length of wall space for his wall fruit trees. The puzzle is to show how the three walls may be built so that each tenant shall have the same area of ground, and precisely the same length of the wall.
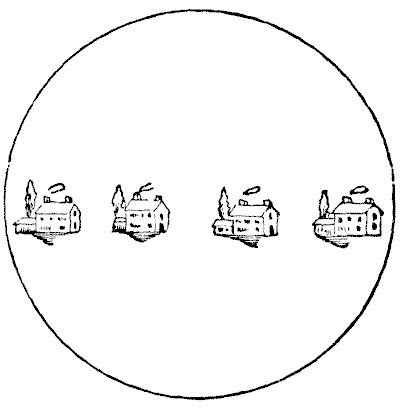
Of course, each garden must be entirely enclosed by its walls, and it must be possible to prove that each garden has exactly the same length of the wall. If the puzzle is properly solved no figures are necessary.
Solutions: 1
This eBook is for the use of anyone anywhere in the United States and most other parts of the world at no cost and with almost no restrictions whatsoever. You may copy it, give it away or re-use it under the terms of the Project Gutenberg License included with this edition or online at http://www.gutenberg.org. If you are not located in the United States, you'll have to check the laws of the country where you are located before using this ebook.