(related to Problem: The Sheep-fold)
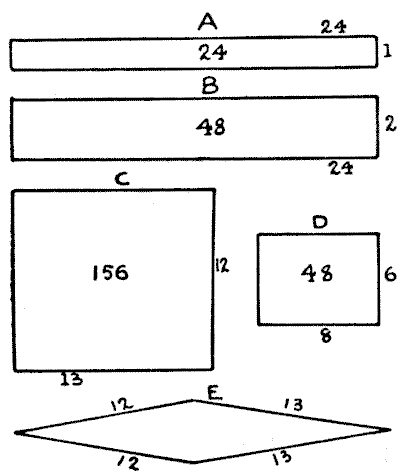
This is the answer that is always given and accepted as correct: Two more hurdles would be necessary, for the pen was twenty-four by one (as in Fig. $A$ below), and by moving one of the sides and placing an extra hurdle at each end (as in Fig. $B$) the area would be doubled. The diagrams are not to scale. Now there is no condition in the puzzle that requires the sheep-fold to be of any particular form. But even if we accept the point that the pen was twenty-four by one, the answer utterly fails, for two extra hurdles are certainly not at all necessary.
For example, I arrange the fifty hurdles as in Fig. $C,$ and as the area is increased from twenty-four "square hurdles" to $156,$ there is now accommodation for $650$ sheep. If it is held that the area must be exactly double that of the original pen, then I construct it (as in Fig. $D$) with twenty-eight hurdles only, and have twenty-two in hand for other purposes on the farm. Even if it were insisted that all the original hurdles must be used, then I should construct it as in Fig. $E,$ where I can get the area as exact as any farmer could possibly require, even if we have to allow for the fact that the sheep might not be able to graze at the extreme ends. Thus we see that, from any point of view, the accepted answer to this ancient little puzzle breaks down. And yet attention has never before been drawn to the absurdity.
This eBook is for the use of anyone anywhere in the United States and most other parts of the world at no cost and with almost no restrictions whatsoever. You may copy it, give it away or re-use it under the terms of the Project Gutenberg License included with this edition or online at http://www.gutenberg.org. If you are not located in the United States, you'll have to check the laws of the country where you are located before using this ebook.