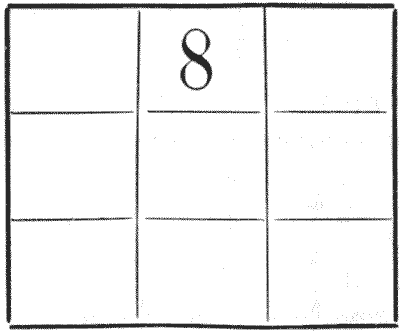
Nearly everybody knows that a "magic square" is an arrangement of numbers in the form of a square so that every row, every column, and each of the two long diagonals adds up alike. For example, you would find little difficulty in merely placing a different number in each of the nine cells in the illustration so that the rows, columns, and diagonals shall all add up $15.$ And at your first attempt you will probably find that you have an $8$ in one of the corners. The puzzle is to construct the magic square, under the same conditions, with the 8 in the position shown.
Solutions: 1