(related to Problem: The Troublesome Eight)
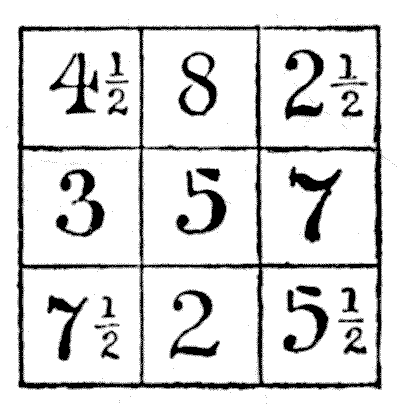
The conditions were to place a different number in each of the nine cells so that the three rows, three columns, and two diagonals should each add up $15.$ Probably the reader at first set himself an impossible task through reading into these conditions something which is not there — a common error in puzzle-solving. If I had said "a different figure," instead of "a different number," it would have been quite impossible with the $8$ placed anywhere but in a corner. And it would have been equally impossible if I had said "a different whole number." But a number may, of course, be fractional, and therein lies the secret of the puzzle. The arrangement shown in the figure will be found to comply exactly with the conditions: all the numbers are different, and the square adds up $15$ in all the required eight ways.