The icosahedron is another of the five regular, or Platonic, bodies having all their sides, angles, and planes similar and equal. It is bounded by twenty similar equilateral triangles. If you cut out a piece of cardboard of the form shown in the smaller diagram and cut halfway through along the dotted lines, it will fold up and form a perfect icosahedron.
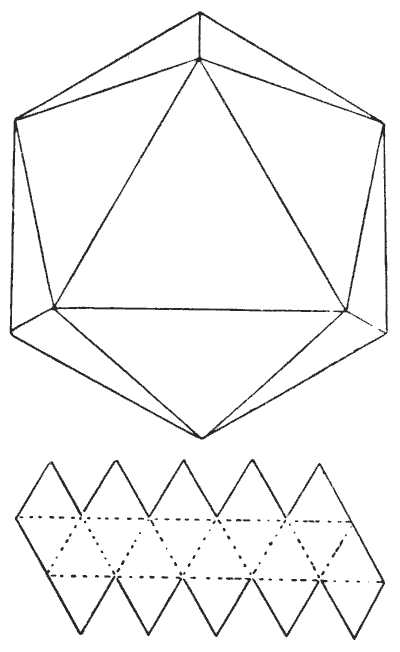
Now, a Platonic body does not mean a heavenly body; but it will suit the purpose of our puzzle if we suppose there to be a habitable planet of this shape. We will also suppose that owing to a superfluity of water, the only dry land is along the edges, and that the inhabitants have no knowledge of navigation. If every one of those edges is 10,000 miles long and a solitary traveler is placed at the North Pole (the highest point shown), how far will he have to travel before he will have visited every habitable part of the planet—that is, have traversed every one of the edges?
Solutions: 1
This eBook is for the use of anyone anywhere in the United States and most other parts of the world at no cost and with almost no restrictions whatsoever. You may copy it, give it away or re-use it under the terms of the Project Gutenberg License included with this edition or online at http://www.gutenberg.org. If you are not located in the United States, you'll have to check the laws of the country where you are located before using this ebook.