Proposition: 2.11: Constructing the Golden Ratio of a Segment

(Proposition 11 from Book 2 of Euclid's “Elements”)

To cut a given straight line such that the rectangle contained by the whole (straight line), and one of the pieces (of the straight line), is equal to the square on the remaining piece.

Let $AB$ be the given straight line.
So it is required to cut $AB$ such that the rectangle contained by the whole (straight line), and one of the pieces (of the straight line), is equal to the square on the remaining piece.

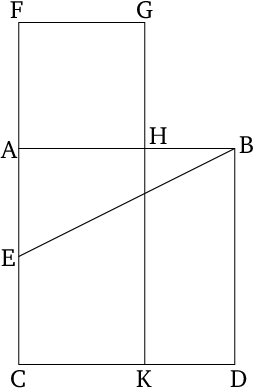
fig11e

Modern Formulation

It is possible to divide a given segment ($\overline{AB}$) into two segments (at $H$) such that the rectangle contained by the whole line ($\overline{AB}=\overline{BD}$), and one segment ($\overline{BH}$) is equal in area to the square on the other segment ($\overline{AH}$). Algebraically, proposition 2.11 solves the equation $\overline{AB}\cdot \overline{BH}=\overline{AH}^{2}$. By setting $a=AB$, we want to find an $x$ such that $a(a-x)=x^{2}$. Specifically,

\[\begin{array}{ccl} a(a-x)&=&x^{2}\\a^{2}-ax&=&x^{2}\\x^{2}+ax&=&a^{2}\\&\Longrightarrow&\\x&=&-\frac{a}{2}(1\pm\sqrt{5})\end{array}.\]

Note that $\gamma=\frac{1+\sqrt{5}}{2}$ is called the Golden Ratio.

Proofs: 1

Proofs: 1
Propositions: 2
Sections: 3

Thank you to the contributors under CC BY-SA 4.0!