Proposition: 2.01: Summing Areas or Rectangles
(Proposition 1 from Book 2 of Euclid's “Elements”)
If there are two straight lines, and one of them is cut into any number of pieces whatsoever, then the rectangle contained by the two straight lines is equal to the (sum of the) rectangles contained by the uncut (straight line), and every one of the pieces (of the cut straight line).
- Let $A$ and $BC$ be the two straight lines, and let $BC$ be cut, at random, at points $D$ and $E$.
- I say that the rectangle contained by $A$ and $BC$ is equal to the rectangle(s) contained by $A$ and $BD$, by $A$ and $DE$, and, finally, by $A$ and $EC$.
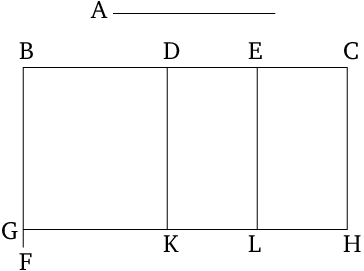
Modern Formulation
Algebraically and more generally, with $a=A=BF,$ $b=BD,$ $c=DE,$ and $d=EC,$ this proposition is a geometric version of the algebraic identity: \[a \,(b+c+d+\cdots) = a\,b + a\,c + a\,d + \cdots.\]
See also distributivity law for real numbers.
Table of Contents
Proofs: 1
Mentioned in:
Sections: 1
Thank you to the contributors under CC BY-SA 4.0! 

- Github:
-

- non-Github:
- @Calahan
- @Casey
- @Fitzpatrick
References
Adapted from CC BY-SA 3.0 Sources:
- Callahan, Daniel: "Euclid’s 'Elements' Redux" 2014
- Prime.mover and others: "Pr∞fWiki", https://proofwiki.org/wiki/Main_Page, 2016
Adapted from (Public Domain)
- Casey, John: "The First Six Books of the Elements of Euclid"
Adapted from (subject to copyright, with kind permission)
- Fitzpatrick, Richard: Euclid's "Elements of Geometry"
